Theoretical Research

We have recently been looking at a series of theoretical areas that revolve around the sustainability and resilience of whole ecosystems under change.

An Inverse Method for Diversity-Stability: Feasibility and Structure

We are currently doing work revisiting longstanding diversity-stability theory but by attacking the problem in a different way (specifically, we employ the linear inverse problem). The classical approach just draws from a statistical universe and fills the community matrix (interaction strengths; IS) and from there estimates stability using well known mathematics (Fig. 1). It is a rational approach but does ignore the fact that many of the randomly drawn IS distributions for a web do not yield an equilibrium. In deed, as diversity grows they approach 0% yield equilibrium.

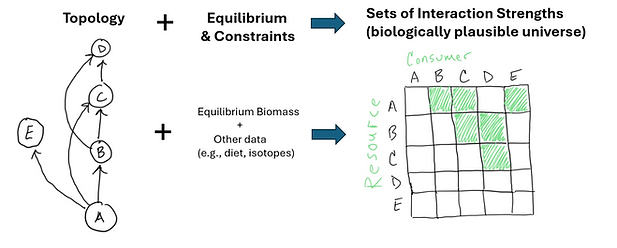
The inverse approach, on the other hand, starts with the equilibrium (and other empirical biological constraints like predators get less energy from prey then prey lose) and then uses this to solve for the interaction strengths (Fig. 2). This ensures the whole food webs are feasible with an equilibrium unlike the classical approach. Notably, the inverse approach is computationally heavy (in Robert May’s time such an approach was not very doable) and draws on bioinformatician approaches in related metabolic network research that makes computations more efficient.

Fig. 1. The Classical “Statistical Universe” Approach. The results may have nothing to do with feasible equilibrium.

A very neat aspect of the inverse approach is that part of the output is interaction strength (IS) data (where interaction strength are the Jacobian or matrix entries here), interaction strengths that meet the constraints and produce the equilibrium. Given enough data they represent real estimates of flows, or often, really distributions of real estimates of flows (Fig., 2; note there is a linear inverse method approach that has used this for estimating flows in food webs for a while already).

Fig. 2. Start with topology and the equilinrium estimates (and other data) and then calculate the interaction strengths that can yield equilibrium under the constraints of the other data. This is often quite under-determined and so yields a universe of biologically plausible interaction strengths.

On a sense thenm the inverse approach takes the equilibrium and filters out ISs that can produce it. The more constraints we have it filters out IS differently and so one can ask how constraints alter IS properties – an interesting aspect of this that has not been done much. As such, when we sample from a distribution of possible flows we can ask questions about the structure of the food web that represents the more or less stable solutions. For a more in-depth explanation and how this can work, see the first paper that was done by a collaboration between post doctoral researcher (Dr. Gabe Gellnerl now works at Stats Canada), Dr. McCann and Dr. Alan Hastings (UC Davis). Check it out in PNAS.

2. Global change and Resilience

At the same time, we are also doing work on how anthropogenic stressors are impacting the structure and stability of ecosystems, often looking at particular ecosystems or particular ecological modules (e.g., competition). Dr. Carling Bieg, for example, has recently looked at how climate change, harvest and nutrients may interact to alter the dynamics and resilience of coral reefs. Here, intriguingly, under environmentally variable conditions stressors interact to produce long transients that can suddenly and precipitously collapse coral to macroalgal or turf algal states.

Although yet published, we are also looking at how environmental forcing can mediate competition using a modified classical Lotka-Volterra competition model. Here, the environmental forcing can significantly alter the coexistence result relative to “endpoint” unforced L-V models. There are cases even, under forcing, where in the unforced versions of the seasonal model yield results in complete contrast to the forced competition. For example, one species cannot invade under both endpoint conditions but still can coexist with noise. Here, the growth rates in the forced model play a much more significant role in coexistence then classical results. It also suggests that as climate change alters season length (e.g., winter) we may expect precipitous changes if such forms of coexistence live in the real world. We note that the conditions are realistic in terms of trade-offs.